Answer:
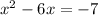
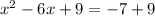
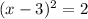
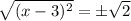
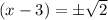
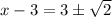
Explanation:
The given quadratic equation is
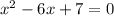
Subtract 7 from both sides.
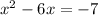 ...(1)
...(1)
If an expression is
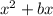 , then we add
, then we add
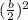 to make it perfect square.
to make it perfect square.
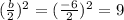
Add 9 on both sides in equation (1).
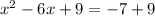
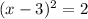
![[\because (a-b)^2=a^2-2ab+b^2]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/2mftkpvzmaczgsxtnle2uhw1gvqjy6ba2v.png)
Taking square root on both sides.
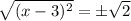
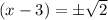
Add 3 on both sides.
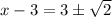
Therefore, the correct order is F, A, D, C, E and B.