Answer:
The range of y is
![[-(5)/(2),(1)/(2)]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/qyo48y47rffj9im3c6pb6baqpup7qpmlwu.png)
Explanation:
Given:
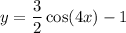
It is cosine function of trigonometry.
We need to find the range of given function. The value of y shows range of function.
y is depends on cosine function.
As we know cosine max/min value is fixed.
y is max when cosine max.
y is min when cosine is min.
Maximum value of cosine = 1
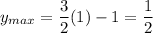
Minimum value of cosine = -1
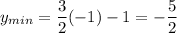
Range of y: [min,max]
Range:
![[-(5)/(2),(1)/(2)]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/qyo48y47rffj9im3c6pb6baqpup7qpmlwu.png)
Hence, The range of y is
![[-(5)/(2),(1)/(2)]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/qyo48y47rffj9im3c6pb6baqpup7qpmlwu.png)