Question

Calculate the side lengths a and b to two decimal places.

Answer 1

Option (a) is correct.

a = 15.68 and b = 19.58

Explanation:

Given: A triangle with some given measurements.

We have to find the values of a and b.

For a triangle ABC , with side opposite to angle A is a , side opposite to angle B is b and side opposite to angle C is c,

Using Sine rule , we have,

`(a)/(\sin A)= (b)/(\sin B)=(c)/(\sin C)`

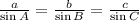
For the given Δ ABC,

∠A = 50° , ∠B = 107°

AB = c = 8 , AC = b and BC = a

Using angle sum property of triangle,

Sum of angles of a triangle is always 180°

So , ∠A + ∠B +∠C = 180°

Solving for ∠C , we get,

∠C = 180° - 107° - 50°

∠C = 23°

Substitute in Sine rule , we have,

`(a)/(\sin 50^(\circ))= (b)/(\sin 107^(\circ))=(c)/(\sin 23^(\circ))`

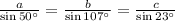
Consider first and last ratios, we have,

`(a)/(\sin 50^(\circ))=(c)/(\sin 23^(\circ))`

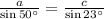
Solving for a, we have,

`a=(\sin \left(50^(\circ \:)\right))/(\sin \left(23^(\circ \:)\right))\cdot \:8`

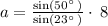
We get , a = 15.68

Consider last two ratios, we have,

`(b)/(\sin 107^(\circ))=(c)/(\sin 23^(\circ))`

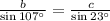
and now solving for b ,

`b=(\sin \left(107^(\circ \:)\right))/(\sin \left(23^(\circ \:)\right))\cdot \:8`

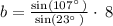
We get , b = 19.58

Thus, option (a) is correct.

a = 15.68 and b = 19.58

Answer 2

missing angle: 180 - 107 -50 = 23 degrees

a = a/ sin(50) = 8/sin(23)

a(sin(23) = 8sin(50)
a*0.3907 = 6.1284
a = 6.1284 / 0.3907 = 15.68

since there is only one answer that has that value for a

the answer is A