Answer:
Option (a) is correct.
a = 15.68 and b = 19.58
Explanation:
Given: A triangle with some given measurements.
We have to find the values of a and b.
For a triangle ABC , with side opposite to angle A is a , side opposite to angle B is b and side opposite to angle C is c,
Using Sine rule , we have,
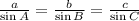
For the given Δ ABC,
∠A = 50° , ∠B = 107°
AB = c = 8 , AC = b and BC = a
Using angle sum property of triangle,
Sum of angles of a triangle is always 180°
So , ∠A + ∠B +∠C = 180°
Solving for ∠C , we get,
∠C = 180° - 107° - 50°
∠C = 23°
Substitute in Sine rule , we have,
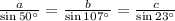
Consider first and last ratios, we have,

Solving for a, we have,
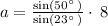
We get , a = 15.68
Consider last two ratios, we have,
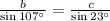
and now solving for b ,

We get , b = 19.58
Thus, option (a) is correct.
a = 15.68 and b = 19.58