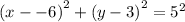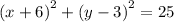Question

Write an equation for the translation of x ^ 2 + y ^ 2 = 25 by 6 units left and 3 units down.

Answer 1

The equation would be: (x + 6)^2 + (y + 3)^2 = 25

This equation will produce a circle. If you add the numbers inside the parenthesis to be squared, you can center of the circle. Thus, translating the shape.

Answer 2

ANSWER

The equation after the translation is

`{(x + 6)}^(2) + {(y - 3)}^(2) = 25`

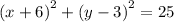
Step-by-step explanation

The given equation is

`{x}^(2) + {y}^(2) = 25.`

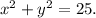
This is an equation of a circle , centered at the origin and with radius

`5 \: units.`

If this circle is translated 6 units to left, then the x-coordinate of the centre will now be at

`x = - 6.`

Also, if the circle is translated 3 units up, then the y-coordinate of the centre will now be at

`y = 3`

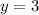
The new centre is now,


`(-6,3).`

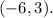
The radius of the circle is not affected after the translation. It is still 5 units.

The new equation can be found using the formula


`{(x - a)}^(2) + {(y - b)}^(2) = {r}^(2)`

Where


`a=-6,b=3,r=5`

The equation now becomes,


`{(x - - 6)}^(2) + {(y - 3)}^(2) = {5}^(2)`


`{(x + 6)}^(2) + {(y - 3)}^(2) = 25`