Question

Nellie is analyzing a circle, y2 + x2 = 25, and a linear function g(x). Will they intersect? y2 + x2 = 25 g(x) graph of the function y squared plus x squared equals 25 x g(x) −7 −2 −6 −1 1 6

Answer 1

Yes, they will intersect at (-5,0) and (0,5).

Explanation:

The equation of circle is

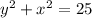`y^2+x^2=25` .... (1)

The graph of g(x) is passing through the points (-7,-2) and (-6,-1).

The equation of g(x) is

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

`y-(-2)=(-1-(-2))/(-6-(-7))(x-(-7))`

`y+2=1(x+7)`

`y=x+7-2`

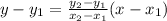
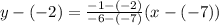
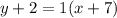
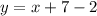
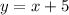`y=x+5` ....(2)

The function g(x) is defined as

`g(x)=x+5`

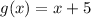
On solving (1) and (2), we get

`(x+5)^2+x^2=25`

`x^2+10x+25+x^2=25`

`2x^2+10x=0`

`2x(x+5)=0`

`x=0,-5`

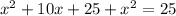
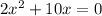
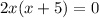
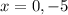
Put x=0 in equation (2).

`y=0+5=5`

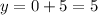
Put x=-5 in equation (2).

`y=-5+5=0`

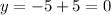
It means both functions intersect at (-5,0) and (0,5).

Answer 2

The linear function is given by the following table:
-7 -2
-6 -1
1 6
The equation of the line is:
y = x + 5
The equation of the circle is:
y2 + x2 = 25
Therefore we have the following system of equations:
y2 + x2 = 25
y = x + 5
The solution is:
x = -5, y = 0
x = 0, y = 5
Therefore, the line and the circle intersect at two points:
(-5, 0)
(0, 5)
Answer:
they will intersect at:
(-5, 0)
(0, 5)