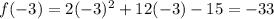Answer:
- Interception on x-axis: (1.06, 0) and (-7.06,0)
- Axis of Symmetry, x=-3
- Minimum Point of y=-33
Explanation:
To describe the graph of the function y=
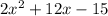 .
.
The function y=
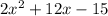 is a quadratic function. All quadratic function have a parabolic curve. The direction to which the parabola opens is determined by the coefficient of
is a quadratic function. All quadratic function have a parabolic curve. The direction to which the parabola opens is determined by the coefficient of
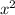 , If the coefficient of
, If the coefficient of
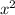 , is positive as in the case above, the graph forms a downward "U" shape.
, is positive as in the case above, the graph forms a downward "U" shape.
The solutions of the function y=
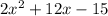 are 1.06 and -7,06, This means the graph intersects the x-axis at points 1.06 and -7.06.
are 1.06 and -7,06, This means the graph intersects the x-axis at points 1.06 and -7.06.
To determine the axis of symmetry of a downward facing parabola,
We use the equation:
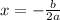
a=2, b=12.
Axis of Symmetry=
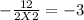
The minimum point is the value of y at the axis of symmetry.