Question

A study of one thousand teens found that the number of hours they spend on social networking sites each week is normally distributed with a mean of 15 hours. The population standard deviation is 2 hours. What is the 95% confidence interval for the mean?

Answer 1

2 standard deviations contain 95% confidence. So thus you would have 4hrs in either direction. So the interval at which we could feel 95% confident is between 11-19hrs. 

Answer 2

The 95% confidence interval for the mean is between 14.88 hours to 15.12 hours.

Explanation:

We have been given:

Sample size or n = 1000

Sample mean = 15 hours

Population standard deviation or s = 2 hours

We will use z distribution to find the confidence interval about the mean.

z value for 95% confidence interval is 1.96.

So, the interval is :

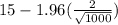`15-1.96((2)/(√(1000)))` and
`15+1.96((2)/(√(1000)))`

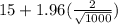
Solving this we get, 14.88 and 15.12

So, the 95% confidence interval for the mean is between 14.88 hours to 15.12 hours.