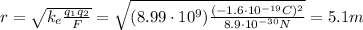The gravitational force on the first electron is equal to its weight:
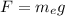
where
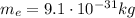
is the electron mass and
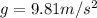
is the gravitational acceleration. Substituting, we find that the gravitational force is
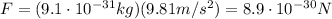
Instead, the electric force exerted by the second electron on the first one is
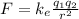
where
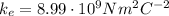
is the Coulomb's constant
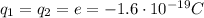
is the charge of each electron
r is the distance between them.
The problem says that the distance r is such that the electric force cancels the gravitational force, so the electric force must be equal to the gravitational force:
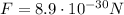
. So, if we use this value in the formula of the electric force, we can calculate the distance r between the two electrons: