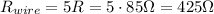Question

A length of wire is cut into five equal pieces. the five pieces are then connected in parallel, with the resulting resistance being 17.0 ω. what was the resistance of the original length of wire before it was cut up? answer in units of ω.

Answer 1

The equivalent resistance of resistors connected in parallel is

`(1)/(R_(eq)) = (1)/(R_1) + (1)/(R_2) + ...`
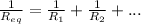
In our problem, we have 5 identical resistor of resistance
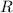
`R`, so their equivalent resistance is

`(1)/(R_(eq)) = 5 ((1)/(R) )`
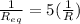
The problem also says that the equivalent resistance is
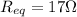
`R_(eq)= 17 \Omega`, so we can find the resistance R of each piece of wire:

`R=5 R_(eq) = 5 \cdot 17 \Omega = 85 \Omega`

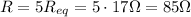
In the initial wire, it's like the 5 pieces are connected in series, so the equivalent resistance of the wire is just the sum of the resistances of the 5 pieces:

`R_(wire) = 5 R = 5 \cdot 85 \Omega = 425 \Omega`