Answer:
1,5 are the points of discontinuity and 5 is the removable discontinuity.
Explanation:
Given : Equation

To find :The point of discontinuity
Solution :
Step 1 : Write the equation

Step 2: To find the point of discontinuity we put denominator =0
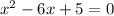
Solving equation by middle term split
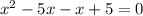
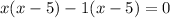
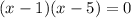

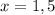
Therefore, the points of discontinuity is 1,5
but if we put in equation
![y=((5-x))/((x^2-6x+5))= [tex]y=((5-x))/((x-1)(x-5))](https://img.qammunity.org/2019/formulas/mathematics/college/mna8njs9n8f4fwpbcvr393t95ejmsqnvvr.png) [/tex]
[/tex]
Since (x-5) factor cancel out in the numerator and denominator therefore, it is a removable discontinuity.
And (x-1) is a infinity discontinuity.
Only (x-5) is removable discontinuity.