Question

What are the points of discontinuity? Are they all removable? Please show your work. y= (5-x)/x^2-6x+5

Answer 1

1,5 are the points of discontinuity and 5 is the removable discontinuity.

Explanation:

Given : Equation
`y=((5-x))/((x^2-6x+5))`

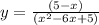
To find :The point of discontinuity

Solution :

Step 1 : Write the equation
`y=((5-x))/((x^2-6x+5))`

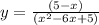
Step 2: To find the point of discontinuity we put denominator =0

`x^2-6x+5=0`

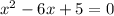
Solving equation by middle term split

`x^2-5x-x+5=0`

`x(x-5)-1(x-5)=0`

`(x-1)(x-5)=0`

`(x-1)=0,(x-5)=0`

`x=1,5`

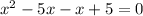
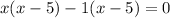
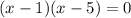
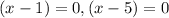
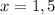
Therefore, the points of discontinuity is 1,5

but if we put in equation

`y=((5-x))/((x^2-6x+5))= [tex]y=((5-x))/((x-1)(x-5))`[/tex]

Since (x-5) factor cancel out in the numerator and denominator therefore, it is a removable discontinuity.

And (x-1) is a infinity discontinuity.

Only (x-5) is removable discontinuity.

Answer 2

We have the following equation:
y = (5-x) / x ^ 2-6x + 5
Rewriting we have:
y = (5-x) / (x-5) * (x-1)
The discontinuity points are:
x = 5
x = 1
x = 5 is removable. For this, we rewrite the function again:
y = (-1 * (5-x)) / (- 1 * (x-5) * (x-1))
y = ((x-5)) / ((x-5) * (1-x))
We cancel similar terms:
y = 1 / (1-x)
Answer:
the points of discontinuity are:
x = 5
x = 1
x = 5 is removable