Question

Can someone please help me with this one question?

Answer 1

It's been awhile since I've worked with infinite series and partial sums, but here are my thoughts:
A. the first 4 terms: -4,
`- (4)/(3)`,
`-(4)/(9)`,
`- (4)/(27)`
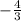
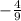
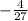
B. In examining the partial sums of the series, it appears that the sequence produced has a limit and therefore the series would be convergent.
C. the limit or sum of the series looks to be -5 Below look at the sequence of partial sums:
-4,
`-5 (1)/(3)`,
`-5 (7)/(9)`,
`-5 (25)/(27)`

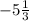
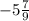
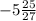
So you can see we're getting closer and closer to -5