Question

A wildlife organization wants to fence off an area of a beach. The organization can only fence 1000 yd2. What length (x) and width (y) should the organization use to use the LEAST amount of fencing as possible? A) length = 50 yards, width = 20 yards B) length = 40 yards, width = 25 yards C) length = 45 yards, width = 222 9 yards D) length = 55 yards, width = 182 11 yards

Answer 1

The correct option is B.

Explanation:

It is given that the total area of a beach is 1000 yd².

We have to find the length (x) and width (y) should the organization use to use the LEAST amount of fencing as possible. It means we have to the find the dimensions for which the parameter is least.

Perimeter of a rectangle is

`S=2* (l+b)`

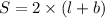
In option 1 the length is 50 yards and width is 20 yards. Perimeter of rectangle is

`S=2* (50+20)=140`

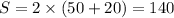
In option 2 the length is 40 yards and width is 25 yards. Perimeter of rectangle is

`S=2* (40+25)=130`

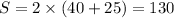
In option 3 the length is 45 yards and width is
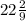`22(2)/(9)` yards. Perimeter of rectangle is

`S=2* (45+22(2)/(9))`

`S=2* (45+(200)/(9))=134.44`

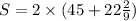
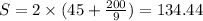
In option 4 the length is 55 yards and width is
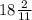`18(2)/(11)` yards. Perimeter of rectangle is

`S=2* (55+18(2)/(11))`

`S=2* (55+(200)/(11))=146.36`

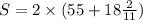
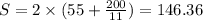
Therefore the least perimeter is 130 when the length is 40 yd and the width is 25 yd.

Answer 2

Of the choices offered, the shortest perimeter is that of an area
C) length = 45 yards, width = 22 2/9 yards

_____
A perimeter shorter yet will be had by an area 10√5 yards by 20√5 yards.