Question

Identify the equations of parabolas that have the directrix x = -4.

Answer 1

The correct answers are as follows:

`x=(y^(2) )/(24) -(7y)/(12) +(97)/(24)`

`x=-(y^(2) )/(16) +(5y)/(8) -(153)/(16)`

`x=(y^(2) )/(32)+ (3y)/(16) +(137)/(32)`

These all have a directrix of -4, while the others have -2, -3, and -6.

You are welcome.

~Kicho [nm68]

Answer 2

Suppose that the point A(x,y) belongs to this parabola. The defining point of the parabola is that the distance between a point F and the directrix. Suppose that the chosen point F is at (a,b). Then, the distance from A to the directrix is |b+4| while the distance from A to the focus is given by the pythagorean theorem:

`d= √((x-a)^2+(y-b)^2)`.
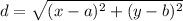
We have that these two have to be equal. Squaring both sides we get:

`b^2+8b+16=(x-a)^2+(y-b)^2`.
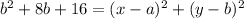
This is the equation that describes all equations of parabolas with that directrix; you just need to choose the focus and substituting a and b will yield the equation.