Answer:
At x=5 it is extraneous
and at
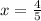 is a verified solution.
is a verified solution.
Explanation:
Given : Expression
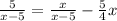
To determine : The solution is extraneous or not?
Solution :
We solve the given expression
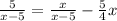
Taking LCM
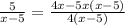
(x-5) cancel from both sides,

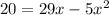
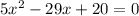
Apply middle term split,
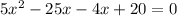
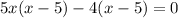
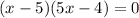
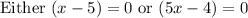
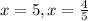
Extraneous is when we get the solution mathematically correct.
Substituting x = 5 gives denominators of 0, which is extraneous.
Substituting
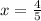 gives a valid equation, so this is the verified solution.
gives a valid equation, so this is the verified solution.