Question

Please help me thank you!!!

Answer 1

There are two acceptable ways of solving this. I'll show both (just in case one of them doesn't align with the information from your textbook).

Option 1 (fast and easy):

The following is the equation for the area of a regular pentagon with side length s.


`A= (s^2)/(4) * \sqrt{5(5+2√(5))}`

Plug s=12 into the equation.


`A= (12^2)/(4) * \sqrt{5(5+2√(5))}`


`\approx 247.7`

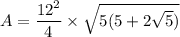
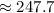
The third choice should be your answer.

Option 2 (much more complicated):

The area of a regular polygon can be solved with the following formula.


`A=\frac{\text{perimeter} * \text{apothem}}{2}`

Let's solve for the apothem.

A pentagon can be divided into 5 congruent isosceles triangles. The vertex angle will be 360/5, or 72 degrees.

An isosceles triangle can be divided into two right triangles. One of the angles of the right triangle will be 72/2, or 36 degrees.

The leg opposite of the 36 degree angle will be 12/2, or 6 inches long.


`\text{apothem}=(6)/(tan(36))`


`\approx 8.26`

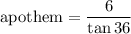
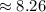
The apothem is about 8.26 inches.
The perimeter is 12*5, or 60 inches.


`A=\frac{\text{perimeter} * \text{apothem}}{2}`


`=(60 * 8.26)/(2)`


`\approx 247.8`

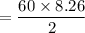
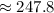
(it seems that we're off by 0.1 due to rounding errors)

The answer is the third choice. Hope this helps! :)