Question

Derek kicks a soccer ball off the ground and in the air, with an initial velocity of 31 feet per second. Using the formula H(t) = −16t2 + vt + s, what is the maximum height the soccer ball reaches? (5 points) 14.2 feet 14.6 feet 15.0 feet 15.3 feet

Answer 1

General Idea:

If we have a quadratic function of the form
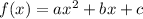`f(x)=ax^(2) +bx+c`, then the function will attain its maximum value only if a < 0 & its maximum value will be at
`x=-(b)/(2a)`.

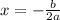Applying the concept:

Comparing the function
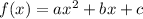`f(x)=ax^(2) +bx+c` with the given function
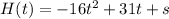`H(t)=-16t^(2) +31t+s`, we get
`a = -16`,
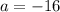`b = 31` and
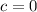`c=0` because initial height of the ball s will be 0.

The maximum height of the soccer ball will occur at
`t=(-b)/(2a)=(-31)/(2(-16)) = (-31)/(-32)=0.96875 seconds`

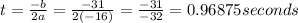
The maximum height is found by substituting
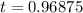`t=0.96875` in the function as below:

`H(0.96875)=-16(0.96875)^2+31(0.96875)`

Conclusion:

The maximum height the soccer ball reaches is 15.0 feet approximately!