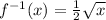Question

Which is the inverse of the function f(x) = 4x2?

Answer 1

`f^(-1)(x)=(1)/(2)√(x)`

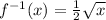
Explanation:

To find the inverse of a function, change the f(x) to a y, switch the places of x and y, then solve for the new y:

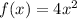`f(x)=4x^2` becomes
`y=4x^2`

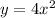
Now switch the places of x and y:

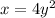`x=4y^2` and solve for the new y:

`(1)/(4)x=y^2`

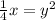
Take the square root of both sides to "undo" the square on the y:

`\sqrt{(1)/(4)x } =y`

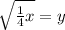
and the square root of 1/4 is 1/2, so we have in the end:

`y=(1)/(2)√(x)`

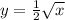
Now you can put it back into inverse function notation since that is, after all, an inverse function:

`f^(-1)(x)=(1)/(2)√(x)`