Question

Prove that for all n in the naturals, n(n+1)(n+2) is divisible by 3

Answer 1

By induction:

It's true for
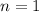
`n=1`, since
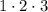
`1\cdot2\cdot3` clearly contains a factor of 3.

Suppose it's true for
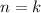
`n=k`, that
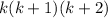
`k(k+1)(k+2)` is divisible by 3. Then


`(k+1)(k+2)(k+3)=\frac{k(k+1)(k+2)(k+3)}k=\frac{3m(k+3)}k`

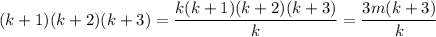
where
`m` is an integer. This reduces to


`\frac{3m(k+3)}k=3m+9\frac mk`

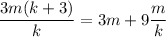
and both terms are clearly multiples of 3. We know that
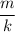
`\frac mk` is an integer since we had set
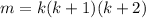
`m=k(k+1)(k+2)` previously, which implies
`m` is a multiple of
`k`. So the statement is true.