Answer:
9 and 11
OR
-9 and -11
Explanation:
let x be the one odd integer
The pattern of numbers go: odd - even - odd - even
The next consecutive odd integer would be x + 2
"Product" means multiplying. Write "the product of two consecutive odd integers with a product of 99" as an algebraic statement:
x(x+2)=99 Distribute over brackets
x² + 2x = 99 Rearrange the equal 0
x² + 2x - 99 = 0
Remember a quadratic equation is ax² + bx + c = 0
(Equate to 0 to use quadratic formula)
State values for quadratic formula from simplified quadratic equation
a = 1; b = 2; c = -99
Use the quadratic formula.

Substitute the values of "a", "b", and "c"
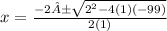 Simplify
Simplify
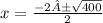 Solve the root
Solve the root
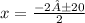
Split the equation at the ±
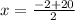
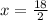
x = 9 Possible integer solution
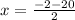
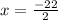
x = -11 Possible integer solution
Integers include all positive and negative whole numbers, and 0. Both positive and negative answers are possible in this problem.
Use "x+2" to get the consecutive integer from the initial possible values for "x".
If x = 9:
x+2 = x+9 = 11
9 and 11
If x = -11:
x+2 = -11+2 = -9
-9 and -11
See if your answers make sense:
9 X 11 = 99
-9 X -11 = 99
Both are possible solutions.