Question

Point g and point h are the same distance from a point f. Which coordinates could be the location of point h? F(3, 2) G(4, 4)

A (1, 2)
B (4, 2)
C (5, 1)
D (2, 5)

Answer 1

b. (4,2)

G is 1 right and 1 up and point B is 1 right and 1 down

Answer 2

Point (5, 1) is the coordinate of point H

Explanation:

Given the point F(3, 2), G(4, 4)

Also point G and point H are the same distance from the point F

We have to find the coordinates of point H.

Using distance formula

`Distance=√((x_2-x_1)^2+(y_2-y_1)^2)`

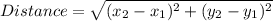
Let the coordinates of point H is (x,y)

GF=FH

`√((3-4)^2+(2-4)^2)=√((x-3)^2+(y-2)^2)`

`5=(x-3)^2+(y-2)^2`

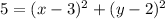
Now the point which satisfied the above equation will the coordinate of point H

A
`(1, 2):(1-3)^2+(2-2)^2=4\\eq 5`

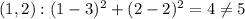
B
`(4, 2):(4-3)^2+(2-2)^2=1\\eq 5`

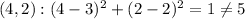
C
`(5, 1):(5-3)^2+(1-2)^2=5=5`

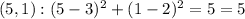
D
`(2, 5):(2-3)^2+(5-2)^2=10\\eq 5`

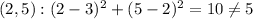
Hence, point (5, 1) is the coordinate of point H