A) To find slope, use the equation:
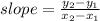
where

and
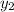
are the x and y values of one coordinate point , and

and
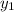
are the x and y values of another coordinate point . Since we are given two coordinate points, (-3,-1) and (4,2), that means we can find the slope using the slope equation.
Let's choose (4, 2) as your
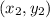
point and (-3, -1) as your
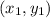
point, but you can switch those if you want! That makes
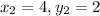
and
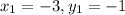
. Plug these values into the slope equation:
 The slope of the line is 3/7.
The slope of the line is 3/7.
B) Remember that the general equation for point-slope form is
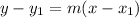
, where m = the slope,

= the x value of a coordinate point
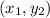
on the line, and
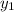
= the y value of the same coordinate point on the line.
You are given (4, 2) as one of the coordinate points. That means

= 4 and
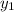
= 2. We found the slope, m =

in part A. Now plug these values into the general equation for point-slope form to find your point-slope form equation:
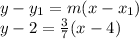 Your point-slope form equation is
Your point-slope form equation is
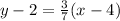 .
.