Question

A triangle has sides of length 11 m, 12 m, and 16 m.

What is the measure of the angle opposite the side that is 16 m long? Round to the nearest degree.

Answer 1

88 degrees.

Explanation:

We have been given that a triangle has sides of length 11 m, 12 m, and 16 m. We are asked to find the measure of the angle opposite the side that is 16 m long.

To find the measure of angle opposite to 16 m side, we will use law of cosines.

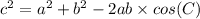`c^2=a^2+b^2-2ab* cos(C)`, where a, b and c represent the side length of triangle. C represents the angle corresponding to side c.

Upon substituting our given values in above formula we will get,

`16^2=11^2+12^2-2* 11* 12* cos(C)`

`256=121+144-264* cos(C)`

`256=265-264* cos(C)`

`256-265=265-265-264* cos(C)`

`-9=-264* cos(C)`

`(-9)/(-264)=(-264* cos(C))/(-264)`

`(-9)/(-264)=cos(C)`

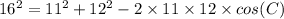
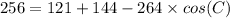
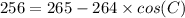
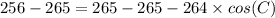
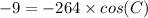
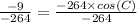
Now we will use inverse cos formula to solve for C.

`cos^(-1)((-9)/(-264))=C`

`88.046356247078^(\circ)=C`

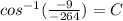
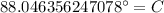
Upon rounding our answer to nearest degree we will get,

`C=88^(\circ)`

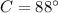
Therefore, the measure of angle opposite to the 16 m long side is 88 degrees.

Answer 2

we know that
the law of cosines formulas established
c²=a²+b²-2*a*b*cos C-----> cos C=[a²+b²-c²]/[2*a*b]
a=11 m
b=12 m
c=16 m
so
cos C=[11²+12²-16²]/[2*11*12]---> cos C=0.0341
C=arc cos (0.0341)-------> C=88.05°

see the attached figure

the answer is
the angle is 88°