Question

A circle has a diameter of 12 units, and its center lies on the x-axis. What could be the equation of the circle? Check all that apply.

(x – 12)2 + y2 = 12
(x – 6)² + y² = 36
x² + y² = 12
x² + y² = 144
(x + 6)² + y² = 36
(x + 12)² + y² = 144

Answer 1

its the 2nd and the 5th

Answer 2

Options 2 and 5.

Explanation:

The standard form of a circle is

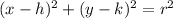`(x-h)^2+(y-k)^2=r^2` ... (1)

where, (h,k) is center and r is radius.

We need to find the circle that has a diameter of 12 units, and its center lies on the x-axis.

`radius=(Diameter)/(2)=(12)/(2)=6`

So, radius of required circle must be 6 and center is in the form of (a,0).

The first equation is

`(x-12)^2+(y)^2=12` .... (2)

On comparing (1) and (2) we get

`h=12,k=0,r=√(12)`

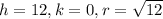
Center of the circle is (12,0) and radius is
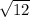`√(12)`. So, option 1 is incorrect.

Similarly,

For equation 2, center of the circle is (6,0) and radius is
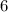`6`. So, option 2 is correct.

For equation 3, center of the circle is (0,0) and radius is
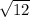`√(12)`. So, option 3 is incorrect.

For equation 4, center of the circle is (0,0) and radius is
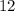`12`. So, option 4 is incorrect.

For equation 5, center of the circle is (-6,0) and radius is
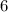`6`. So, option 5 is correct.

For equation 6, center of the circle is (-12,0) and radius is
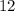`12`. So, option 6 is incorrect.

Therefore, the correct options are 2 and 5.