Question

What is the measure of ∠P, to the nearest degree?

Answer 1

You can solve for C using the law of cosines.

P, Q, and R are the angles of the triangle and p, q, and r are the lengths of the sides of the triangle opposite of the angles. That means p = 10ft, q = 12ft, and r=5ft. The law of cosines states that:

`p^2 = q^2+r^2-2qr(cosP) \\ q^2 = p^2+r^2-2pr(cosQ) \\ r^2 = p^2+q^2-2pq(cosR)`

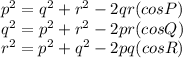
Since we're looking for the measure of angle P, we would use the first equation,
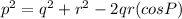
`p^2 = q^2+r^2-2qr(cosP)`. Plug the values we have for the sides of the triangle into the equation and solve for P:

`p^2 = q^2+r^2-2qr(cosP)\\ 10^(2) = 12^(2) + 5^(2) - 2(12)(5)(cosP)\\ 100 = 144 + 25 - 120cosP\\ 120cosP = 69\\ cosP = 0.575\\ P = cos^(-1)(0.575)\\ P \approx 55\°`

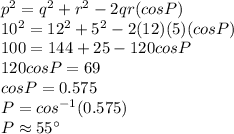The measure of angle P is about 55°.