Answer:
The simplified value of the given expression is -16-10i.
Explanation:
The given expression is
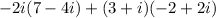
We need to convert the expression into the form a + bi, where a and b are rational numbers.
Using distributive property we get

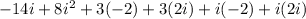
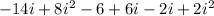
Combine like terms.
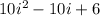
Substitute
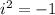 ,
,

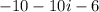
Combine like terms.

Therefore the simplified value of the given expression is -16-10i.