Question

Factor the algebraic expression below in terms of a single trigonometric function. sin 2x + sin x - 2

Answer 1

The factored form is (sin x +2)(sin x-1)

Explanation:

We have been given the trigonometric function
`\sin^2 x +\sinx-2`

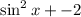
We can factor this by AC method. In AC method we multiply the term a and c and then write the middle term b in such a way that the sum/difference is equal to the product 'ac'

Using the method, we can write sinx as 2sinx -sinx

`\sin^2 x +2\sinx-\sin x-2`

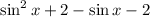
Now, we group the first two terms and the last two terms

`(\sin^2 x +2\sinx)+(-\sin x-2)`

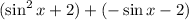
Now, we take GCF from each group

`\sin x(\sin x +2)-1(\sin x+2)`

Factor out (sinx+2)

`(\sin x +2)(\sin x-1)`

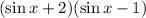
Therefore, the factored form is (sin x +2)(sin x-1)

Answer 2

The factor form is
`(\sin x+2)(\sin x-1)`

Explanation:

Given : Algebraic expression
`\sin^2x+\sin x-2`

To find : Factor the algebraic expression in terms of a single trigonometric function ?

Solution :

Algebraic expression
`\sin^2x+\sin x-2`

Let
`\sin x=y`

So,
`y^2+y-2`

To factor the expression we equate it to zero,

`y^2+y-2=0`

Apply middle term split,

`y^2+2y-y-2=0`

`y(y+2)-1(y+2)=0`

`(y+2)(y-1)=0`

Substitute the value of y,
`y=\sin x`

`(\sin x+2)(\sin x-1)=0`

The factor form is
`(\sin x+2)(\sin x-1)`