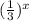Question

Consider the exponential function f(x) = 3(1/3)^x and its graph

Which statements are true for this function and graph? Check all that apply.

The initial value of the function is 1/3.

The growth value of the function is 1/3.

The function shows exponential decay.

The function is a stretch of the function f(x) = (1/3)^x

The function is a shrink of the function f(x) = 3^x

One point on the graph is (3, 0).

Answer 1

The base of the function is One-third.

The function shows exponential decay.

The function is a stretch of the function f(x) = (one-third) Superscript x.

Explanation:

I think!

Answer 2

An exponential function is of the form f(x)=a
`b^(x)`

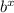
where a ≠0, b > 0 , b ≠1, and x is any real number.

when b > 1, the graph increases.

when 0 < b < 1, the graph decreases.

a = initial value,r = growth or decay rate

x = number of time.

The given Exponential function is

`f(x)=3((1)/(3))^x`

Among the options given the ones which are true for the given function are:

The growth value of the function is 1/3

The function shows exponential decay

The function is a stretch of the function f(x) =
`((1)/(3))^x`