Answer: The correct option is (d)
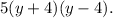
Step-by-step explanation: We are given to find the least common multiple of the following polynomials:
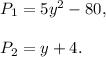
The LEAST COMMON MULTIPLE of two or more polynomials is a polynomial of the least degree that is divisible by all the other polynomials.
We have
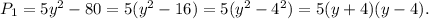
Therefore, the least common multiple of the polynomials will be
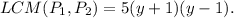
Thus, (d) is the correct option.