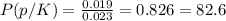Question

The guidance department has reported that of the senior class, 2.3% are members of key club, K, 8.6% are enrolled in AP physics, P, and 1.9% are enrolled in both. Determine the probability of P given K, to the nearest tenth of a percent.

Answer 1

P(P|K) = 82.6%.

P(P|K) = P(K and P)/P(K) = 1.9%/2.3% = 0.019/0.023 = 0.8261 = 82.6%

Answer 2

The question is related to conditional probability .

It is given in the question that, the guidance department has reported that of the senior class, 2.3% are members of key club, K, 8.6% are enrolled in AP physics, P, and 1.9% are enrolled in both.

So we have ,

`image`

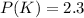
We have to use the following formula

`P(p/K) = ( P(p \cap K) )/(P(K))`

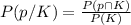
Substituting the values, we will get

`P(p/K) = (0.019)/(0.023) = 0.826= 82.6%`