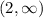Question

Let h(t) = -16t2nd power + 64t + 80 represent the height of an object above the ground after t seconds. Determine the number of seconds it takes to achieve its maximum height. Justify your answer.

State the time interval, in seconds, during which the height of the object decreases. Explain your reasoning.

Answer 1

Given equation is

`h(t) = -16t^2 + 64t + 80`

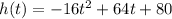
We have to find the time interval by which height is maximum.

We start with differentiating .

Differentiating h(t) ,

`image`

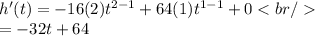
Differentiating again

`h''(t)= -32(1)t^(1-1) +0 = -32 <0`

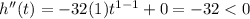
Since on double differentiating , we are getting a negative number, so the height is maximum.

And to find the time of maximum height, we set h'(t) to 0, that is

`image`

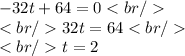
In second part, the height is decreasing means slope, h'(t) is less than 0. That is,

`image`

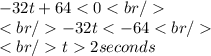
So the required time interval is

`(2 , \infty)`