To find the length of the arc, you want to multiply the circumference of the circle by the fraction of the degrees in a full circle (360°) that the angle creating the arc PQ covers.
The angle of a complete circle is 360°. Since you are given all the angles except for the angle creating the arc PQ, you can subtract your given angles angles from 360° to get your missing angle:
360°-150°-73°-65° = 72°
The angle creating the arc PQ is 72°. That means the fraction of the full circle that the arc takes up/covers is:
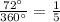
. The arc is 1/5 the entire arc/circumference of the circle.
Now find the circumference. Remember that the equation for circumference is

, where c=circumference and r=radius. You're given that the radius, r = 6.48 in. Plug that into the circumference equation to find the circumference of the circle:

Now multiply the fraction that the arc covers by the circumference. You know the arc is 1/5 the circumference:
 The length of the arc PQ is about 8.1 in.
The length of the arc PQ is about 8.1 in.