Question

Suppose that a student is doing the photoelectric effect experiment by shining light onto a metallic surface and measuring the speed of the ejected electrons. if the intensity of the incident light is doubled without changing the type of light, the kemax of the electrons will be ______________ original.

Answer 1

The maximum kinetic energy of the electrons will be the same as the original.

In fact, in the photoelectric effect one photon hits the surface of the metal and gives its energy to one photoelectron, according to the equation:

`hf = \phi + K`
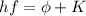
where
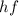
`hf` is the photon energy, with h being the Planck constant and f the frequency of the light,
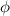
`\phi` is the work function (the energy needed to extract the photoelectron from the metal) and
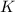
`K` is the kinetic energy of the photoelectron.

So the kinetic energy of the photoelectron is

`K= hf - \phi`
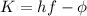
and we can see that this value doesn't change when we change the intensity of the light: in fact, if the intensity of the light is double, then the energy of the single photon hf remains the same (we have only doubled the number of photons, but not the energy of the single photon), so the kinetic energy of the electrons doesn't change.