Question

Give the demensions of a right triangle and a pararalogram with the same area

Answer 1

If a parallelogram and a triangle have the same area, this means 1 of the dimensions of the parallelogram will be half the dimension of the triangle.

Ex : triangle b= 10, h= 4
A = 40/2 or 20 square units

Parallelogram b = 5, h= 4
A = 5 x 4 or 20 square units

Answer 2

We are going to form a triangle of base 10 inches ans height 5 finches; also, the eight of our triangle will be the width of our rectangle (a rectangle is a parallelogram). First, we are going to use the area of a triangle formula:
`A= (1)/(2) bh`
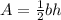
where

`A` is the area in square inches

`b` is the base of the triangle

`h` is the height of the triangle
We know that
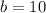
`b=10` and
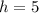
`h=5`, so lets replace those values in our formula:

`A= (1)/(2) (10)(50)`

`A= (1)/(2)(50)`

`A=25`

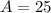
Now that we have the area of our triangle, we are going to use the area of a rectangle formula:
`A=wl`
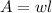
where

`A` is the area in square inches

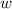
`w` is the width of the rectangle

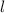
`l` is the length of the rectangle
Since the width of our rectangle is equal to the height of our triangle,
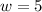
`w=5`. Also, we know for our problem that the area of our triangle and the area of our triangle must be equal, so
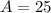
`A=25`. Lets replace those values in our formula to find the length of our rectangle:

`A=wl`

`25=5l`

`l= (25)/(5)`

`l=5`

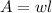
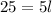
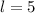
We can conclude that the dimensions of our triangle are: base=10 inches and height= 5 inches, and the dimensions of our parallelogram are: width= 5 inches and length= 5 inches.