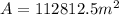The perimeter for this case is given by:
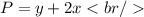
Substituting values we have:
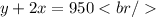
The area is given by:

Writing the area based on a variable we have:
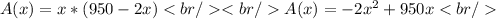
We derive the area to obtain the maximum of the function:
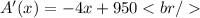
We equal zero and clear x:
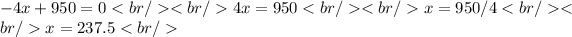
Then, the other dimension is given by:
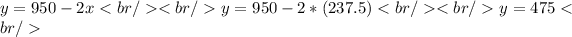
Finally the maximum area is:
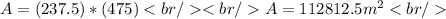
Answer:
The length and width of the plot that will maximize the area are:
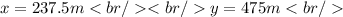
The largest area that can be enclosed is: