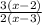Question

(05.02)

Simplify completely quantity 6 x squared minus 54 x plus 84 over quantity 8 x squared minus 40 x plus 48 divided by quantity x squared plus x minus. (2 points)

Answer 1

The answer to this is that 3(x-2) / 2(x-3) as the simplified form of the given equation.

Answer 2

`(3(x-2))/(2(x-3))`

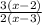
Explanation:

The given expression is

`(6x^(2) -54x+84)/(8x^(2)-40x+48 ) / (x^(2) +x-56)/(2x^(2)+12x-32)`

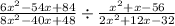
We need to factor each quadratic expression

`6x^(2) -54x+84`

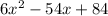
First, we extract the GCF 6:

`6(x^(2)-9x+14 )`

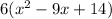
Then, we look for two numbers which product is 14 and which sum is 9, thos numbers are 7 and 2, so the factored expression is

`6(x-7)(x-2)`

`8x^(2) -40x+48`

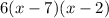
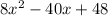
We do the same process,

`8(x^(2) -5x+6)`

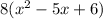
We need to find two numbers which product is 6 and which sum is 5, those numbers are 3 and 2

`8(x-3)(x-2)`

`x^(2) +x-56`

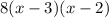
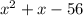
We have to find two numbers which product is 56, and which difference is 1, those numbers are 8 and 7

`x^(2) +x-56=(x+8)(x-7)`

`2x^(2) +12x-32=2(x^(2)+6x-16 )=2(x+8)(x-2)`

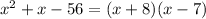
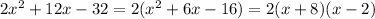
Replacing all factors in the given expression, we have

`(6(x-7)(x-2))/(8(x-3)(x-2)) / ((x+8)(x-7))/(2(x+8)(x-2)) \\(3(x-7))/(4(x-3)) / ((x-7))/(2(x-2)) \\(3(x-7))/(4(x-3)) * (2(x-2))/((x-7)) =(3(x-2))/(2(x-3))`

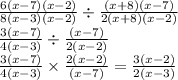
Therefore, the answer is

`(3(x-2))/(2(x-3))`