Answer: C) ∠B = ∠B' = 57° and ∠C = ∠C' = 33°
Explanation:
GIven:- In ΔABC, ∠A = 3x, ∠B = 2x - 3, and ∠C = x + 3.
In ΔA'B'C' ∠A' = 2x + 30, ∠B' = x + 27, and ∠C' = 1/2x + 18
By angle sum property in ΔABC
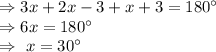
⇒ ∠A =3(30)=90°
∠B=2(30)-3=57°
∠C=30+3=33°
By angle sum property in ΔA'B'C'
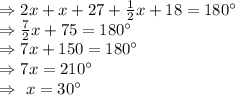
∠A'=2(30)+30=90°
∠B'=30+27=57°
∠C'=

therefore, C) ∠B = ∠B' = 57° and ∠C = ∠C' = 33° gives ΔABC∼ΔA'B'C by the AA criterion.