Question

Given: KLMN is a trapezoid m∠N = m∠KML

ME ⊥ KN , ME =
`3√(5)`, KE = 8, LM:KN = 3:5
Find: KM, LM, KN, Area of KLMN

I know that KM is
`√(109)`

Answer 1

Answer: KM= square root of 109, LM=48/5, KN=16, A=192sqr root of 5/5

Explanation:

Answer 2

The length of sides KM, LM and KN are
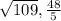`√(109), (48)/(5)` and 16 respectively. The area of KLMN is
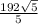`(192√(5))/(5)` square unit.

Explanation:

According to given information: KLMN is a trapezoid, ∠N= ∠KML,
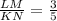`(LM)/(KN)=(3)/(5)`, ME ⊥ KN, KE=8
`ME=3√(5)`.

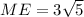Use pythagoras theorem is triangle EKM

`Hypotenuse^2=base^2+perpendicular^2`

`(KM)^2=(KE)^2+(ME)^2`

`(KM)^2=(8)^2+(3√(5))^2`

`KM^2=64+9(5)`

`KM=√(109)`

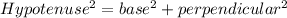
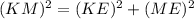
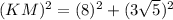
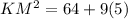
Let angle N and angle KML be θ.

Since angle KML and angle MKE are alternate interior angles, therefore angle MKE is θ.

In triangle KME,

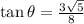`\tan\theta=(3√(5) )/(8)` .... (1)

In triangle KNE,

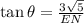`\tan\theta=(3√(5) )/(EN)` .... (2)

Equate (1) and (2),

`(3√(5) )/(8)=(3√(5) )/(EN)`

`EN=8`

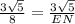
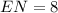
The length of side KN is

`KN=KE+EN=8+8=16`

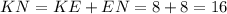
Sides LM:KN are in the ratio 3:5. Let the side lengths are 3x and 5x respectively.

`5x=16`

`x=(16)/(5)`

`3x=3* (16)/(5)=(48)/(5)`

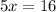
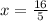
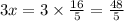
The area of KLMN is

`Area=(1)/(2)(b_1+b_2)h`

`A=(1)/(2)* (LM+KN)* ME`

`A=(1)/(2)* ((48)/(5)+16)* 3√(5)`

`A=(192√(5))/(5)`

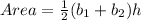
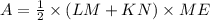
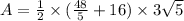
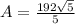
Therefore length of sides KM, LM and KN are
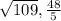`√(109), (48)/(5)` and 16 respectively. The area of KLMN is
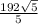`(192√(5))/(5)` square unit.