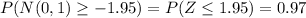Question

A national restaurant chain claims that their servers make an average of $12.85 in tips per hour, with a standard deviation of $2.15. The servers at the restaurant chain's location in Dallas make an average of $8.65 in tips per hour. Given that the data is approximately normal, find the probability that a server, chosen at random, will make more than $8.65 in tips per hour.

Answer 1

We need to calculate the probability:

`P(N\geq 8.65)`
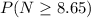
wherein N is the normal law.

`P((N-12.85)/(2.15)\geq (8.65-12.85)/(2.15))`
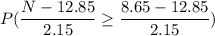
Simplifying the right hand side of the inequality we get:

`P((N-12.85)/(2.15)\geq -1.95`
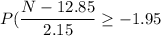
The above formula can be written in the form:

`P(N(0,1)\geq -1.95)`

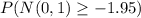
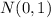
`N(0,1)` is the normal law with mean 0 and standard deviation 1.
Using the table of the values we find the probability

`P(N(0,1)\geq -1.95)=P(Z\leq1.95)=0.97`

Answer 2

97%

Explanation: