Question

Each week Peggy drives two routes, route X and route Y. One week she drives route X three times and route Y twice. she drives a total of 144 miles that week. Another week she drives route X twice and route Y five times. she drives a total of 217 miles that week. Find the length of each route

Answer 1

x = 26 , y = 33

Step-by-step explanation:

3x + 2y = 144 (1)

2x + 5y = 217 (2)

3x + 2y = 144

(divide the equation by 3)

x + (2/3)y = 48

x = 48 - (2/3)y

Plug into (2)

2(48 - (2/3)y) + 5y = 217

96 - (4/3)y + 5y = 217

11y/3 = 217 - 96

11y/3 = 121

y = 121×3/11

y = 33

x = 48 - (2/3)y

x = 48 - (2/3)(33)

x = 48 - 22

x = 26

Answer 2

Ok, great to have you! I will finally answer your question.
This seems to be a system of equations. I solve most of mine on Desmos.
Let us write two equations to model this:

`3x+2y=144`

`2x+5y =217`
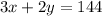
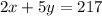
We get the graph. Note the intersection at (26,33).
That means that route X is 26 miles long,and route Y is 33 miles long!.
Hope this helps.