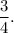Question

Circle 1 has center (−6, 2) and a radius of 8 cm. Circle 2 has center (−1, −4) and a radius 6 cm. What transformations can be applied to Circle 1 to prove that the circles are similar? Enter your answers in the boxes. Enter the scale factor as a fraction in simplest form

Answer 1

"Circle 1 has center (−6, 2) and a radius of 8 cm. Circle 2 has center (−1, −4) and a radius 6 cm. What transformations can be applied to Circle 1 to prove that the circles are similar? Enter your answers in the boxes. Enter the scale factor as a fraction in simplest form"

The circles are similar because the transformation rule (x+5 y-6) can be applied to Circle 1 and then dilate it using a scale factor of 3/4

Answer 2

Answer: The required transformations are

a translation of (x + 5, y - 6) and a dilation by a scale factor of
`(3)/(4).`

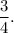
Step-by-step explanation: Given that Circle 1 has centre (−6, 2) and a radius of 8 cm whereas Circle 2 has centre (−1, −4) and a radius 6 cm.

We are to find the transformations that can be applied to Circle 1 to prove that the circles are similar.

The two circles are shown in the attached figure below.

We can prove two figures similar if one or more similarity transformations (reflections, translations, rotations, dilation) can be found so that one figure is mapped onto another.

Since we are to prove the similarity of two circles, so a translation and a scale factor will work here.

Since the centre is shifted from (-6, 2) to (-1, -4), so the translation rule of the centre is

(-6 + 5, 2 - 6) = (-1, -4), i.e., (x, y) ⇒ (x+5, y - 6).

Now, the radius of Circle 1 is 8 units and radius of Circle 2 is 6 units, so the scale factor of dilation will be

`S=\frac{\textup{radius of the dilated circle 2}}{\textup{radius of the original circle 1}}=(6)/(8)=(3)/(4).`

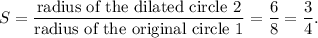
Thus, the required transformations are

a translation of (x + 5, y - 6) and a dilation by a scale factor of
`(3)/(4).`