Question

a square swimming pool is surrounded by a cement walkway with a uniform width.The swimming pool has a side length of (x-2) feet. The side length of the entire square area including the pool and the walkway is (x+1) feet. Write an expression for the area of the walkway. Then find the area of the cement walkway when x=7 feet.

Answer 1

Start by drawing a picture (see attached image).

To find the area of the walkway, you need to subtract the area of the pool (the smaller, dark blue square) from the area of the entire square (pool + walkway) to get the area of the walkway (light blue area). This is because the light blue area will be what is left over after you take away the dark blue area from the area of the entire big square (light blue + dark blue).

1) Start by writing an expression for the area of the entire square minus area of the pool.
Remember the equation for the area of a square is
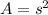
`A = s^(2)`, where A = area of square and s = length of one side of the square.
We are given that the side of the entire square including walkway and pool is s = (x+1)ft. Plug that into the equation for the area of a square to get the expression for the area of the entire square:

`A = s^(2)\\ A = (x+1)^(2)`

We are also given that the side length of the swimming pool is s = (x-2)ft. Plug that into the equation for the area of a square to get the expression for the area of the pool:

`A = s^(2)\\ A = (x-2)^(2)`

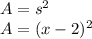
Now subtract the area of the pool (
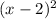
`(x-2)^(2)`) from the area of the entire square (
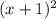
`(x+1)^(2)`) to get your expression for the area of the walkway.
Expression for the area of the walkway:
`(x+1)^(2) - (x-2)^(2)`

2) Since you know that x = 7ft, you can solve your expression for the area of the walkway. Plug x into your expression:

`(x+1)^(2) - (x-2)^(2)\\ = (7+1)^(2) - (7-2)^(2)\\ = (8)^(2) - (5)^(2)\\ = 64 - 25\\ = 39 \: ft^(2)`

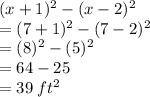The area of your walkway is
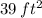`39 \: ft^(2)`.