Question

An exterior angle measure of a regular polygon is given. Find the number of its sides and the measure of each interior angle. 40° The regular polygon has ___ sides and each of its interior angles measures____  °.

Answer 1

Since this polygon is a regular polygon, that means its interior and exterior angles are all the same.

1) The sum of the exterior angles of a polygon is always 360°. The measure of each exterior angle for a polygon with "n" sides can be found using the equation: measure of each exterior angle =
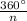
`(360\°)/(n)`. Since you know the measure of each exterior angle is 40°, plug that into the equation and solve for n, the number of sides:

`measure \: of\: each\: exterior\: angle = (360\°)/(n) \\ 40\° = (360\°)/(n) \\ n = (360\°)/(40\°)\\ n = 9`

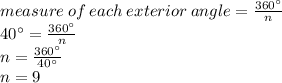The polygon has 9 sides.

2) The equation for the measurement of an interior angle is found by dividing the sum of all the interior angles by the number of sides (which is equal to the number of angles in a polygon). The sum of all the interior angles =
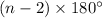
`(n-2) * 180\°`. The number of sides = n. Divide the sum by n to get the measurement of your interior angle.
That means the measurement of the interior angle =
`((n-2) * 180\°)/(n)`.

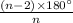
From step 1, you know the number of sides = 9. Plug that into your equation for the measurement of the interior angle:

`((n-2) * 180\°)/(n)\\ = ((9-2) * 180\°)/(9)\\ = (1260\°)/(9) \\ = 140\°`

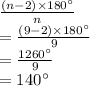Each interior angle measures 140°.

Answer 2

Sum of all exterior angles = 360°.

Number of sides = 360 ÷ 40 = 9

Each interior angle = 180 - 40 = 140°.

Answer: The regular polygon has 9 sides and each of its interior angles 140°