Question

Evaluate the geometric series or state that it diverges. one ninth 1 9plus+startfraction 7 over 81 endfraction 7 81plus+startfraction 49 over 729 endfraction 49 729plus+startfraction 343 over 6561 endfraction 343 6561plus+...

Answer 1

The series converges, and its sum is 1/2.

If r > 1, the series is divergent. If r < 1, the series is convergent. In our sequence, r, the common ratio we multiply by to get the next term, is 7/9; therefore it is convergent.

To find the sum of a convergent series, we use the formula
a/(1-r), where a is the first term and r is the common ratio. We then have
1/9÷(1-7/9) = 1/9÷2/9 = 1/9×9/2 = 1/2

Answer 2

In the given geometric series, r, the common ratio is 7/9; therefore the series is convergent.

Explanation:

We are given the geometric series:

`(1)/(9) + (7)/(81) + (49)/(729) + (343)/(6561) + ...`

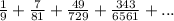
The general geometric series is in the for
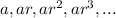`a, ar, ar^2, ar^3, ...`, where a is the first term and r is the common ratio.

Comparing with the given geometric series, we have,
`a = (1)/(9) \text{ and }r = (7)/(9)`

If r > 1, the series is divergent.

If r < 1, the series is convergent.

In the given geometric series, r, the common ratio is 7/9; therefore the series is convergent.