Question

The product of two positive numbers is 1024. what is the minimum value of their sum?

Answer 1

Let the two positive numbers are x , y and there sum is s
So,
x y = 1024 ⇒⇒⇒⇒ (1)
And S = x + y ⇒⇒⇒⇒ (2)
by substituting from (1) at (2) with the value of y = 1024/x

∴ s = x +
`(1024)/(x)`

Differentiating both sides with respect to x to find the minimum value of the sum and equating to zero

∴
`(ds)/(dx) = 1 - (1024)/( x^(2) ) = 0`

solve the last equation for x
∴
`1 - (1024)/( x^(2) ) = 0`

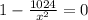
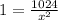
`1 = (1024)/( x^(2) )` ⇒⇒⇒ *x²
∴ x² = 1024
∴
`x = \pm √(1024) = \pm 32`
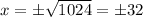
taking the positive number as stated in the problem

x = 32

So, The numbers are 32 , 32
And theire mimimum sum = 32 + 32 = 64