Question

A rectangular piece of cardboard can be turned into an open box by cutting away identical squares from each corner and folding up the resulting flaps. The cardboard is 12 inches long and 12 inches wide. a) Write an expression for the length of the box in terms of x (the length of each square you cut away). b) Write an expression for the width of the box in terms of x. c) Write an expression for the Volume of the box in terms of x. d) Find the dimensions of the box that will yield the maximum volume.

Answer 1

After removing the square corners, you're left with a cross shape that folds into a cuboid with base dimensions
`12-x` by
`12-x`, and height
`x`. The volume of this box is
`x(12-x)^2`.

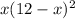
Writing this as a function, we can take the derivative to find the critical points and determine the value of
`x` that maximizes the volume:


`image`


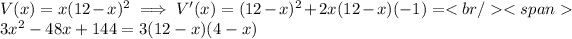
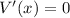
`V'(x)=0` when
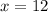
`x=12` or
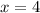
`x=4`. But
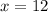
`x=12`, the cut we try to make isn't a cut; the piece of cardboard stays flat and unchanged. So the volume is maximized when
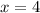
`x=4` (you can verify that the derivative behaves accordingly; that is,
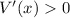
`V'(x)>0` for
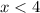
`x<4` and
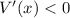
`V'(x)<0` for
`x>4`).

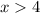
The largest volume of the box is then
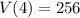
`V(4)=256` cubic inches.