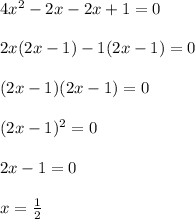Question

A quadratic equation is shown below:

25x2 + 10x + 1 = 0


Part A: Describe the solution(s) to the equation by just determining the radicand. Show your work. (5 points)


Part B: Solve 4x2 − 4x + 1 = 0 by using an appropriate method. Show the steps of your work, and explain why you chose the method used. (5 points)

Answer 1

Part A)

The given equation is:


`25 x^(2) +10x+1=0`

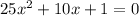
The radicand or discriminant(d) of the equation will be:


`d=(10)^(2)-4(25)(1) \\ \\ d=100-100 \\ \\ d=0`

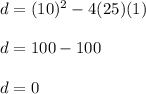
Since the discriminant is equal to 0, the given quadratic equation has only 1 root. In other words we can say the the given equation is a perfect square.


Part B)

The given equation is:


`4 x^(2) -4x+1=0`

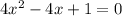
We can solve this expression by factorization. Factors of middle term are to be made in such a way that their product equals the product of first and third term and sum is equal to the middle term i.e. product should be 4x² and sum should be -4x.
So the two such terms are -2x and -2x. Using the factors and simplifying the equation by taking common we get:


`4 x^(2) -2x-2x+1=0 \\ \\ 2x(2x-1)-1(2x-1)=0 \\ \\ (2x-1)(2x-1)=0 \\ \\ (2x-1) ^(2)=0 \\ \\ 2x-1=0 \\ \\ x= (1)/(2)`