Question

Solving a Quadratic Equation by Completing the Square Solve x2 + 8x = 33 by completing the square. Which is the solution set of the equation? {–11, 3} {–3, 11} {–4, 4} {–7, 7}

Answer 1

Answer: The Answer To This Problem is {–11, 3} .Which Is Option A!!!

Answer 2

Divide the coefficient of x by 2 then square the quotient.
Add the result to both sides of the equation.


`x^2 + 8x = 33`

`x^2 + 8x + ((8)/(2))^2 = 33 + ((8)/(2))^2`

`x^2 + 8x + 4^2 = 33 + 4^2`

`x^2 + 8x + 16 = 33 + 16`

`x^2 + 8x + 16 = 49`

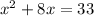
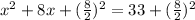
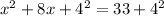
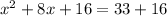
Factor the left-hand side.


`(x + 4)^2 = 49`

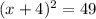
Square both sides.


`x + 4 = √(49)`

Subtract both sides by 4.


`x = -4`
`± √(49)`

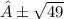
Simplify.


`x = -4`
`± 7`
So, x can either equal -4 + 7 or -4 - 7

So, the answer is {-11, 3}

NOTE: You're probably seeing a strange A in the equations. I tried to fix it, but I couldn't. Sorry about that.