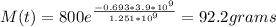Question

How much of an 800-gram sample of potassium-40 will remain after 3.9 x 109 years of radioactive decay?

Answer 1

`N_(t) = N_(o) e^{ \frac{-693t}{ t_{ (1)/(2) } } }`

Where,

`N_(t) = Quantity remaining after some time`

`N_(o) = Original qunatity`

`t_{ (1)/(2) } = Half life = 1.251* 10^(9) years for potassium-40`

Substituting;

`N_{} =800* e^{ (-0.693*3.9* 10^(9) )/(1.251* 10^(9) ) }` = 151.83 g

Answer 2

Ans: Amount of K-40 remaining = 92.2 g

Given:

Initial mass of potassium-40 = M₀ = 800 g

Time, t = 3.9 *10⁹ years

To determine:

The mass of potassium-40 (M(t)) that will remain after time 't'

Step-by-step explanation:

The radioactive decay equation is given as:

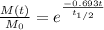`(M(t))/(M_(0) ) = e^{(-0.693t)/(t_(1/2) ) }` ----(1)

where t1/2 is the half-life of K-40 = 1.251*10⁹ years

Substitute for M₀, t and t1/2 in equation(1):

`M(t) = 800 e^{(-0.693*3.9*10^(9) )/(1.251*10^(9) ) } = 92.2 grams`